Case Study - Hexagonal Grids for Terracotta RPG
A case study of how I built a hexagonal grid system for procedural territory generation.
When building complex game systems, sometimes the most elegant solutions come from isolating a single component and perfecting it before integration. My experience with hexagonal grids for procedural territory generation proves exactly that.
Quick Links:
I've been building a solo RPG that combines deterministic rogue-like mechanics with AI-enhanced narrative generation. One of the core challenges I faced was creating believable, dynamic faction territories during world generation. These are regions of power and influence that emerge naturally from the interaction of different factions, without relying purely on AI or random noise.
This case study examines my decision to build a hexagonal grid-based territory system in isolation before integrating it into the main game, and why I chose algorithmic expansion over AI generation.
Why Build Features in Isolation?
When building complex systems like procedural world generation, I've learned to resist the urge to develop features directly in the main codebase. Instead, I create standalone exploration projects that let me iterate rapidly without risking the stability of the core application.
For the territory system, I built a dedicated hex grid visualizer using PixiJS and React. This isolation gave me several advantages:
- Faster iteration cycles: No need to boot the full game stack to test territory expansion rules
- Visual debugging: Immediate visual feedback made it easy to spot issues with expansion algorithms
- Risk containment: Experimentation couldn't break existing gameplay systems
- Easier testing: Simpler to test edge cases and boundary conditions
This approach mirrors how I've seen successful teams work on large-scale systems; build the risky, experimental components separately, validate the approach, then integrate once you're confident.
Why Hexagonal Grids Over X/Y Coordinates?
The decision to use hexagonal grids instead of simpler rectangular coordinates wasn't arbitrary. Hexagonal grids provide specific advantages for strategic gameplay:
Uniform neighbor distances: Every adjacent hex is equidistant from the center, unlike square grids where diagonal movement is √2 times longer than orthogonal movement. This creates more balanced, natural-feeling territory expansion.
Consistent neighbor count: Each hex has exactly six neighbors (except edges), making expansion rules simpler and more predictable than square grids where corner vs. edge tiles behave differently.
Natural organic shapes: Territory boundaries formed on hexagonal grids tend to look more organic and believable than the straight lines and right angles of rectangular grids.
While rectangular grids are simpler to implement (just x,y pairs), hexagonal grids better serve the gameplay goal of creating territories that feel like they emerged from actual conflict and expansion rather than arbitrary geometric constraints.
Generating Faction Territories Through Algorithmic Expansion
The core challenge was this: given a world with multiple factions, each with different attributes (power level, chaos tendency, moral alignment), how do you generate believable territory boundaries that feel like they resulted from actual conflict and expansion?
My first instinct was to use AI. After all, LLMs are great at generating plausible content. Instead, I chose an algorithmic approach inspired by actual warfare and expansion patterns:
Each faction starts from a seed hex and expands outward based on its attributes:
- Power determines expansion rate (higher power = more frequent expansion)
- Chaos influences whether factions prefer empty territory or conflict
- Alignment affects targeting priority (Evil factions prioritize Good factions, etc.)
This creates emergent, believable patterns. A powerful but chaotic faction expands aggressively and creates jagged borders through constant conflict. An orderly faction with moderate power expands methodically into empty space, creating smooth boundaries.
What do the Hexes Represent?
One of the key insights from building this system was keeping the hex abstraction flexible. In Terracotta RPG, the same hex grid system can represent radically different things depending on the world context:
- High fantasy: Each hex might be a city district or village cluster
- Science fiction: Each hex could represent a solar system or space sector
- Modern drama: Hexes might map to neighborhoods, office buildings, or transit stations
By keeping the territory logic separate from what the territories represent, the system becomes reusable across different game modes and settings. The expansion algorithms don't care whether they're simulating warring kingdoms or competing mega-corporations. The rules work the same way.
Hexagons in Code
Once you commit to hexagonal grids, you need a coordinate system. Unlike rectangular grids where (x, y) is the obvious choice, hexagons have several coordinate systems to choose from. I went with axial coordinates using q and r.
Axial Coordinates: q, r, and the Hidden s
In axial coordinates, each hex is identified by two values:
q: Position along the "column" axisr: Position along the "row" axis
Here's the clever part: hexagons actually exist in a 3D cube coordinate system where q + r + s = 0 always holds true. You can derive s at any time:
const s = -q - r;
Finding all six neighbors is just adding constant offsets:
AXIAL_DIRECTIONS = [
(1, 0), // East
(1, -1), // Northeast
(0, -1), // Northwest
(-1, 0), // West
(-1, 1), // Southwest
(0, 1), // Southeast
]
function get_neighbors(q, r):
return [(q + dq, r + dr) for (dq, dr) in AXIAL_DIRECTIONS]
function hex_distance(q1, r1, q2, r2):
s1 = -q1 - r1
s2 = -q2 - r2
return (abs(q1 - q2) + abs(r1 - r2) + abs(s1 - s2)) / 2
This constraint is what makes hexagonal math work elegantly. Distance calculations, neighbor finding, and path-finding all become simpler when you can work with cube coordinates instead of trying to force hexagons into a rectangular worldview.
Why Not Just Use x, y?
You could map hexagons to a rectangular coordinate system, but you'd be fighting the geometry constantly. With rectangular coordinates:
- Neighbor offsets change depending on whether you're on an even or odd row
- Distance calculations require special-case logic
- Converting between screen space and grid space becomes more complex
With axial coordinates, finding the six neighbors of any hex is just adding six constant offsets to (q, r). Distance is (abs(q) + abs(r) + abs(s)) / 2. The math aligns with the structure.
World Sizes and Faction Counts
The hex grid radius dramatically affects world complexity. I settled on the following world sizes, each supporting a different number of competing factions:
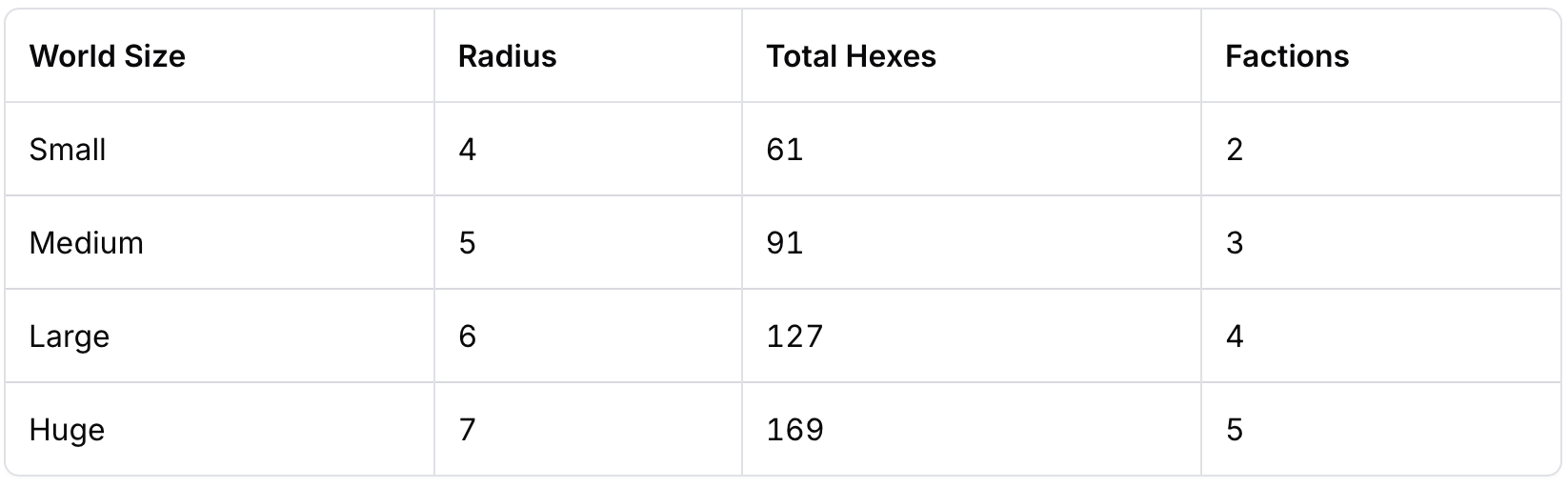
The total hex count follows the formula: 3r² + 3r + 1 where r is the radius.
function get_total_hexes(radius):
return 3 * radius * radius + 3 * radius + 1
# Examples:
get_total_hexes(1) # 7 hexes - barely a village
get_total_hexes(4) # 61 hexes - small kingdom
get_total_hexes(7) # 169 hexes - continent-spanning empire
How Does the Hex Grid Size Affect the Story?
The size of the hex grid world fundamentally shapes the types of stories and conflicts that emerge. Here's how different world sizes create distinct narrative environments, using high fantasy settings as examples:
Tiny World (37 hexes, 1 faction)
- Narrative Focus: Internal politics, status games, and personal rivalries
- Example Setting: A secluded elven enclave hidden in an ancient forest
- Conflict Type: Court intrigue, succession disputes, and personal vendettas
- Quest Themes: Uncovering secrets, gaining influence, navigating social hierarchies
- Key Dynamic: With only one dominant faction, existential threats are rare; characters compete for power and status within a stable system
In a tiny world, you're essentially exploring a microcosm—perhaps a single city-state or an isolated community. Without external threats, characters focus on climbing social ladders, forming alliances, and outmaneuvering rivals. Think of it as a face-slapping drama where the stakes are personal rather than world-ending.
Small World (61 hexes, 2 factions)
- Narrative Focus: Binary opposition, clear moral or ideological contrasts
- Example Setting: The Last Bastion of humanity versus the encroaching Chaos Horde
- Conflict Type: Direct confrontation, border disputes, espionage
- Quest Themes: Defending territory, converting neutrals, sabotaging the enemy
- Key Dynamic: Classic "us versus them" storytelling with clear battle lines
Small worlds create focused narratives with clear stakes. Perhaps one faction represents order (an aging empire) while the other embodies change (rebel alliance). Or maybe it's a contrast in methods. For example, sword-wielders versus magic-users, who forced to share limited resources in a single continent. The binary nature creates tension through its simplicity.
Huge World (169 hexes, 5 factions)
- Narrative Focus: Epic, sprawling narratives with multiple simultaneous conflicts
- Example Setting: Game of Thrones-style continent with five great houses and many minor ones
- Conflict Type: Simultaneous wars, succession crises, existential threats
- Quest Themes: Uniting divided realms, navigating complex loyalties, surviving chaos
- Key Dynamic: Constant instability as no faction can secure enough territory to feel safe
In huge worlds, the narrative scope expands dramatically. Like Three Kingdoms China or Game of Thrones, these settings feature multiple major powers in constant flux. The sheer size creates a sense of epic scale where heroes' journeys can span vastly different cultures and landscapes. Unlike tiny worlds where status games dominate, huge worlds feature genuine existential threats where entire factions might be wiped out.
Each world size creates its own strategic and narrative texture while using the same underlying hex grid mechanics. The beauty of this system is how it scales from intimate dramas to continent-spanning epics simply by adjusting the radius parameter.
Expansion and Conquering
The territory generation system starts simple. Each faction gets a root seed hex, their initial foothold in the world. From there, the expansion algorithm simulates rounds of territorial growth and conflict until all hexes are claimed.
Root Seeds: Starting Positions
Root seeds are the anchor points for each faction. During setup, these are placed on the hex grid (either manually in the visualizer or procedurally in the game). Each seed hex represents:
- The faction's home territory (can never be conquered)
- The starting point for all connected territory
- A reference point for checking territorial cohesion
The algorithm enforces a critical rule: only hexes connected to a faction's root seed count as valid territory. If expansion creates disconnected regions (perhaps through aggressive enemy expansion cutting through your territory), those orphaned hexes are automatically reclaimed as neutral ground.
function get_connected_hexes(seed_hex_id, territory_id, hex_ownership):
connected = new Set()
queue = [seed_hex_id]
connected.add(seed_hex_id)
while queue is not empty:
current = queue.remove_first()
neighbors = get_neighbors(current)
for neighbor in neighbors:
neighbor_id = f"{neighbor.q},{neighbor.r}"
# Only traverse hexes owned by this territory
if hex_ownership[neighbor_id] == territory_id and
neighbor_id not in connected:
connected.add(neighbor_id)
queue.append(neighbor_id)
return connected
function remove_orphaned_hexes():
for seed in territory_seeds:
valid_hexes = get_connected_hexes(
seed.hex_id,
seed.territory_id,
hex_ownership
)
# Unclaim any hex owned by this territory that isn't connected
for hex_id, owner_id in hex_ownership.items():
if owner_id == seed.territory_id and hex_id not in valid_hexes:
delete hex_ownership[hex_id] # Becomes neutral again
The Core Expansion Loop
Here's the basic algorithm structure:
graph TD
A[Start Round] --> B{Any unclaimed hexes?}
B -->|No| Z[End: Finished Phase]
B -->|Yes| C[Select Attacker by Weighted Power]
C --> D[Get Empty Adjacent Hexes]
C --> E[Get Enemy Adjacent Hexes<br/>excluding root seeds]
D --> F{Roll Chaos Check}
E --> F
F -->|Prefers Conflict| G[Apply Alignment Priority<br/>Conflict Mode]
F -->|Prefers Expansion| H[Apply Alignment Priority<br/>Expansion Mode]
G --> I{Target Found?}
H --> I
I -->|Yes| J[Claim Target Hex]
I -->|No| A
J --> K[Run Disconnection Check]
K --> L[Remove Orphaned Hexes]
L --> A
Each round, one faction gets to expand by a single hex. The selection continues until every hex on the map is claimed.
Power, Luck, and Entropy
Power determines how often a faction gets to act. The algorithm uses weighted random selection—if total power across all factions is 1000, and your faction has 400 power, you have a 40% chance of being selected each round.
This creates natural momentum: stronger factions expand faster but aren't guaranteed to dominate. A weaker faction might get a lucky streak early and claim strategic positions that shift the entire balance of power.
The randomness creates enough variation that each world feels unique.
Capturing Nodes and Territorial Death
Factions can claim:
- Empty hexes (peaceful expansion), OR
- Enemy territory (conquest), as long as it's not a root seed
Whether a faction prefers conquest or expansion depends on their chaos and alignment attributes (detailed below).
After each conquest, the disconnection check runs. Using breadth-first search from each root seed, the algorithm identifies all hexes still connected to their faction's seed. Any owned hexes that can't be reached become neutral.
Example: If Blue faction aggressively pushes through Red territory, splitting Red's holdings in two, all Red hexes on the disconnected side immediately become neutral. Blue (or another faction) can then claim them.
This prevents "exclaves" and creates dynamic borders where overextension leads to sudden territorial collapse.
Orderly vs Chaotic: Conflict Preference
Chaos determines whether a faction prefers peaceful expansion or active conflict:
- Orderly: 10% chance to prefer enemy neighbors over empty space
- Neutral: 20% chance to prefer enemy neighbors over empty space
- Chaotic: 40% chance to prefer enemy neighbors over empty space
Each round, the faction rolls against this percentage. If the roll succeeds AND enemy neighbors exist, the faction becomes aggressive that round. Otherwise, it prefers peaceful expansion into empty hexes.
This creates visible personality in territorial shapes:
- Orderly factions form smooth, cohesive regions (they usually avoid conflict)
- Chaotic factions have jagged, contested borders (they actively seek enemies)
function select_target(attacker, empty_neighbors, enemy_neighbors):
# Step 1: Chaos determines aggression this round
chaos_threshold = {
"Chaotic": 0.4,
"Neutral": 0.2,
"Orderly": 0.1
}
prefers_conflict = random() < chaos_threshold[attacker.chaos]
# Step 2: Build priority lists based on alignment
target_priority = []
if attacker.alignment == "Good":
evil_targets = [h for h in enemy_neighbors if h.alignment == "Evil"]
neutral_targets = [h for h in enemy_neighbors if h.alignment == "Neutral"]
good_targets = [h for h in enemy_neighbors if h.alignment == "Good"]
target_priority = prefers_conflict
? [evil_targets, empty_neighbors, neutral_targets, good_targets]
: [empty_neighbors, evil_targets, neutral_targets, good_targets]
else if attacker.alignment == "Evil":
good_targets = [h for h in enemy_neighbors if h.alignment == "Good"]
neutral_targets = [h for h in enemy_neighbors if h.alignment == "Neutral"]
evil_targets = [h for h in enemy_neighbors if h.alignment == "Evil"]
target_priority = prefers_conflict
? [good_targets, neutral_targets, evil_targets, empty_neighbors]
: [empty_neighbors, good_targets, neutral_targets, evil_targets]
else: # Neutral
target_priority = prefers_conflict
? [enemy_neighbors, empty_neighbors]
: [empty_neighbors, enemy_neighbors]
# Step 3: Pick first available target from priority list
for pool in target_priority:
if pool is not empty:
return random_choice(pool)
return null # No valid targets (shouldn't happen)
The Player Experience We're Building Toward
In Terracotta RPG, players transmigrate into procedurally generated worlds where every run tells a different story, yet every story feels grounded in coherent rules. The territory system serves this vision by creating worlds that feel lived-in before the player arrives.
When a player starts a new run, they don't need to understand the expansion algorithm to grasp what happened. They see a map where a Chaotic Evil empire has aggressively carved out territory by targeting Good neighbors, leaving jagged, contested borders. They see Orderly Good kingdoms with smooth, methodical expansion patterns that suggest defensive, cautious leadership. They see Neutral city-states filling the gaps between larger powers.
This creates emergent backstory. The territorial map becomes a historical artifact that tells players what kind of world they've entered before the first turn of gameplay.
How Technology Reflects Design Goals
Every technical decision in this system serves a specific player experience goal:
Hexagonal grids create depth without complexity. Six neighbors instead of eight (square grids) makes territorial relationships easier to grasp while still supporting interesting expansion patterns.
Chaos and alignment attributes create faction personality without requiring complex AI prompting. A Chaotic Good faction doesn't need an LLM to understand it should hunt Evil neighbors. Instead, the algorithm handles it through simple probability checks.
Root seed anchoring prevents exclaves and creates realistic territorial collapse. When a faction overextends, losing territory follows game rules players can learn and predict.
The result is a system where emergence comes from determinism and entropy, not randomness. The territories feel organic because they emerged from conflict rules, not because an AI imagined them.
Key Learnings
Building this feature in isolation allows me to take away several lessons:
1. Build risky features separately: The hex grid visualizer let me iterate on expansion rules without risking the main codebase. I tested dozens of chaos/alignment combinations and power ratios before finding the right balance. This would have been painful in the integrated environment.
2. Visual debugging is invaluable: Watching territories expand in real-time revealed edge cases I never would have caught through unit tests alone. Seeing a faction collapse due to disconnection made the mechanic immediately understandable.
3. Constraints create coherence: By limiting world sizes to specific increments (4-7 hex radius) and tying faction counts to world size, I eliminated whole categories of balance problems.
Try It Yourself
The hex grid territory visualizer is live at my website. You can:
- Adjust faction attributes (power, chaos, alignment)
- Place root seeds manually
- Watch territories expand in real-time
- Experiment with different world sizes
- See how chaos and alignment affect expansion patterns
The code demonstrates a broader principle for AI application development: use deterministic systems for game mechanics, reserve AI for content generation. This creates the best of both worlds. Reliable, master-able gameplay enhanced by dynamic, unpredictable narrative.
As I integrate this system into Terracotta RPG, these territories will become the backdrop for player stories. The algorithmic expansion creates believable starting conditions, then AI-driven narrative fills in the details of why these factions exist, what they believe, and how they interact with the player.
That's the power of choosing the right tool for each job: algorithms for coherence, AI for creativity, and the discipline to know which is which.
I'm currently exploring procedural generation and AI-driven narrative. If you're working on similar systems or have thoughts about balancing deterministic systems with non-deterministic AI generation, I'd love to hear from you.
Feel free to reach out at avi.santoso@gmail.com to discuss game design, procedural generation techniques, or how we might collaborate on future projects.